Unibuy DEX Protocol v0.1

Abstract​

Unibuy is an order book-like exchange protocol based on the constant product formula. In centralized exchange order books, prices are user-defined single points, whereas in the Unibuy order books, prices are specified as price ranges along the constant product curve.

Unibuy protocol sets up two mirrored one-way liquidity pools for each token pair, providing a trading experience similar to Uniswap’s two-way liquidity pools. The effect of one-way trading pairs is that a small price spread is automatically maintained between the two mirrored pairs, which effectively prevents sandwich attack, a common problem in current DEX trading.

User orders are generally divided into two types: maker order and taker order. A maker order sells a specified amount of $\small token_0$ within a specified price range. The lower bound of the price range, after being mirrored, must be lower than the current price of the associated mirror pair, ensuring that the maker order does not get filled immediately. A taker order buys a specified amount of $\small token_0$ or sells a specified amount of $\small token_1$, provided that the highest acceptable price limit is above the current price. Taker orders always execute immediately.

A one-way trading pair always sells $\small token_0$ and buys $\small token_1$. In the mirror pair, the definitions of $\small token_0$ and $\small token_1$ are reversed. From the perspective of the maker order users, a maker order is always selling $\small token_0$ and buying $\small token_1$. From the perspective of the taker order users, it is selling $\small token_1$ and buying $\small token_0$. The maker and taker orders act as counterparties to each other, and the buying and selling of the same token are completed through two linked mirror trading pairs.

Taker orders always drive the price of $\small token_0$ up along the constant product curve, whereas maker orders may drive the price of the current trading pair down. While a user's maker order is fully or partially filled, if the token price reverses, this maker order does not passively buy back the sold $\small token_0$ as in the Uniswap protocol. This design can address the impermanent loss problem faced by liquidity providers in Uniswap.

Unibuy protocol introduces a range liquidity rebalancing mechanism and a forward compensation mechanism for maker orders, which resolve internal arbitrage problem that might exist in maker order transaction, and allow for the aggregation of maker order liquidity across different price ranges.

Liquidity in the Unibuy protocol is provided entirely by maker orders. There is no automated market maker (AMM) role as in Uniswap, so all trading fees paid by taker orders become the revenue of Unibuy protocol.

1. Introduction​

Uniswap$^{[1,2,3,4]}$ protocol has undergone continuous upgrades from v1/v2 to v3/v4, constantly improving and optimizing the specific implementation of the Constant Product Automated Market Maker (CPAMM) mechanism. These improvements have enhanced capital efficiency for liquidity providers and established Uniswap as the leading DEX in the DeFi space. Its core mechanism has been widely imitated by many Web3 projects. However, Uniswap-type DEXs also face a number of issues.

1.1 Protocol Revenue Issue​

The Uniswap protocol requires liquidity providers to supply liquidity for user transactions. In return, liquidity providers receive the majority of the transaction fees paid by users, while the DEX project itself only receives a small portion of it. Uniswap has implemented a switch to enable transaction fee splitting, which can only be activated through governance voting. In practice, this has led to situations where Uniswap is unable to generate revenue from user transactions.

1.2 Impermanent Loss Issue​

Although the constant product AMM mechanism solves the problem of automatic pricing in token trading, it inevitably introduces the difficult problem of impermanent loss$^{[5]}$. Professional market makers can partially mitigate impermanent loss by continuously monitoring the status of trading pairs and dynamically adjusting the distribution of liquidity in response to price changes. However, common Web3 users lack the tools and expertise to do this. If they provide liquidity for a long time without timely adjustments, the limited returns from market making often fail to offset the suffered impermanent loss. This discourages ordinary users from participating as liquidity providers and negatively impacts the overall liquidity of DEXs.

1.3 Sandwich Attack Issue​

Uniswap trading pairs are bidirectional, meaning that the selling price of a token is also its buying price. After a user executes a trade, the token price moves along the constant product curve predictly, making the transaction vulnerable to sandwich attacks. In such an attack, a malicious attacker front-runs a user's large-value exchange by placing a transaction in the same direction, causing the token price to move unfavorably for the user. Following the user's transaction, the attacker initiates a reverse transaction to arbitrage the price spread. Numerous such attacks can be found in on-chain transactions. While many countermeasures have been proposed$^{[6,7]}$, they are not universally applicable.

The Unibuy protocol can natively solve the above three major issues based on its design mechanism.

1.4 Unibuy Protocol Solutions​

The Unibuy protocol adopts an order book mechanism similar to the centralized exchanges (CEXs), eliminating the role of liquidity providers (market makers). All trading fees are retained by the Unibuy protocol operators, which inherently solves the issue of transaction fee distribution.

Similar to CEX order books, liquidity in the Unibuy protocol is provided by user's maker orders waiting to be filled. Once a taker order is executed, the received $\small token_1$ keep staying in the pool rather than being re-used in further trades, as is the case in constant product market makers. Since there is no role of market makers, the protocol naturally avoids the issue of impermanent loss caused by significant price fluctuations.

The Unibuy protocol must be of unidirectional trading pairs due to its order book design. To support two-way token trading (i.e., both buy and sell), two mirrored unidirectional pairs are deployed. This internal technical design does not impact the user trading experience. However, it results in a useful side effect: the buy and sell prices for the same token in the mirrored pairs naturally keep a spread. This inherent spread effectively protects against sandwich attacks. Even if an attacker front-runs a trade, they cannot manipulate the token price in the mirrored pair and thus cannot profit from a reverse transaction, rendering the attack meaningless.

1.5 Differences from CEX Order Books​

Despite similarities, the Unibuy protocol’s order book differs from that of the centralized exchanges.

In CEXs, when a user places a buy or sell order, it is immediately filled if there is a matching order in the order book, this is called a taker order. If no match is found, the order is added to the order book and published to all traders, awaiting future matching. Each order has a single fixed price, and the entire order book forms a set of discrete price points on the price axis.

In contrast, Unibuy orders specify a price range rather than a single price. Within this range, the specified token amount is automatically filled according to the constant product curve. The Unibuy protocol automatically determines whether the order results in a taker order, a maker order, or a partial fill, based on user-defined parameters. If an order can only be partially filled, the unfilled portion can either be converted to a maker order awaiting a future taker, or be terminated immediately after a partial fill, depending on the user's preference. All the liquidity of maker orders with various price range are aggregated together to form the liquidity for taker orders.

Unibuy does not adopt the typical CEX rule of matching orders based on price and time priority. Instead, it aggregates all maker order liquidity to fill taker orders according to the constant product formula.

Unibuy maker orders are publicly visible on-chain and represent real user orders, avoiding issues common to CEXs such as fake orders or iceberg orders that may mislead users. Due to blockchain characteristics, such as block time period and transaction competition, placing deceptive orders on-chain carries high risk and limited advantage.

CEXs usually incentivize makers with lower exchange fee rate compared to takers. In the Unibuy protocol, maker orders are always free, whether filled or not.

Some previous projects, like EtherDelta$^{[8]}$ and Serum$^{[9]}$, have attempted to implement on-chain order book DEXs. However, these projects mainly copied traditional CEX order books on-chain, without technical innovation or integration with blockchain-specific features. Due to various reasons, they were ultimately not successful. A viable on-chain order book requires technical breakthroughs and innovation.

1.6 Unibuy Protocol​

Unibuy is a decentralized exchange protocol offering an order book functionality. Integrating the constant product AMM mechanism with key features of CEX order books, it aggregates all user's maker orders as the liquidity for taker orders, without requiring a complex on-chain order matching engine. This approach aims to explore a practical path toward realizing a fully on-chain order book DEX.

Unibuy protocol sets up two mirrored one-way trading pairs for a pair of trading tokens. Each pair supports the selling of a single token, and two one-way trading pairs are linked together to provide the buy/sell service for the token pair.

The concept of using two mirrored unidirectional pairs in a DEX was previously explored by FeSwap$^{[10]}$, which used this design to offer a zero-fee DEX with market-making returns. Although the project lacked promotion and users, it continued to operate and accumulated a fair amount of on-chain transactions. While Unibuy’s mirrored pair design appears similar on the surface, it is fundamentally a different implementation, specifically designed to enable a technically sound on-chain order book.

To aggregate the liquidity of maker orders from different users, price ranges, and order batches, Unibuy introduces the liquidity rebalancing mechanism and the forward compensation mechanism for maker orders. This allows maker order liquidity to be aggregated to provide liquidity for taker orders, avoiding the need for a complex CEX-style matching and clearance mechanisms. The following sections describe Unibuy’s technical solution in detail.

2. Unibuy DEX Protocol​

2.1 Basics of Range Liquidity​

In Uniswap v3/v4, to improve the capital efficiency of liquidity provision, liquidity providers (LPs) can specify the price range within which they provide liquidity. This avoids allocating capital to price intervals that are unlikely to reach, thereby avoiding capital wasting. Uniswap introduces the concept of $\small tick$, which are discrete integers that can correspond to token prices in a trading pair. Using $\small ticks$, liquidity can be divided into multiple distinct price ranges, allowing liquidity within the same range to aggregate and collectively participate in token trading.

When the price of a trading pair moves and crosses into a new price range, the protocol adjusts the liquidity parameters accordingly, so that in each price range, the trading pair still follows the constant product formula, but with different liquidity parameters.

By using $\small ticks$ to define the price range for liquidity provision, LPs only need to allocate capital to cover a specific price interval. Compared to Uniswap v1/v2, which requires liquidity over the entire range of $\small (0, \infty)$, this approach allows the same amount of capital to support more effective trading liquidity. This is the core idea behind Uniswap’s concept of "concentrated" or "virtual" liquidity.

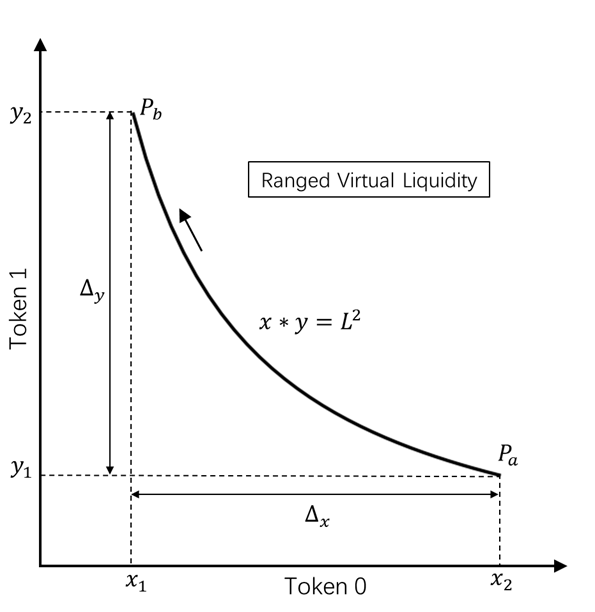
Figure 1 illustrates a price range, also known as a $\small tick$ interval, denoted as $\small (P_a, P_b)$. Assuming the virtual liquidity constant is $\small L$, and the virtual amounts of the two tokens in the trading pair are $\small x, y$, the constant product formula is expressed as:

Formally, this formula has the same expression as the constant product formula used in Uniswap v1/v2, but the meaning is different. In Uniswap v1/v2, $\small x, y$ represent the real amounts of the two tokens, and the constant $\small L$ remains unchanged across the entire price space.

However, in Uniswap v3/v4 and in the Unibuy protocol, $\small x$ and $\small y$ are the virtual amounts of the two tokens, and the constant $\small L$ remains unchanged only within the $\small tick$ interval. While crossing different tick intervals, the value of $\small L$ usually varies.

Within the Unibuy protocol, what is of real significance is the change in the virtual amount of two tokens across the price range, denoted as $\small \Delta x$ and $\small \Delta y$, which satisfy the following formula:

In the Unibuy protocol, when a user places a maker order to sell an amount $\small \Delta x$ of an asset within the price range $\small (P_a, P_b)$, the corresponding virtual liquidity $\small L$ for that price range can be calculated using equation (2.1.2). The protocol internally records the user's provided virtual liquidity $\small L$. By simply adding together the virtual liquidity of different users within the same price range, the virtual liquidity aggregation is achieved.

When a user places a taker order, since the virtual liquidity constant $\small L$ is already known, the price change of the trading pair can be calculated based on the amount of asset $\small \Delta y$ they wish to sell or the amount of asset $\small \Delta x$ they wish to buy, using equation (2.1.3) or (2.1.2) respectively, thereby determining the corresponding $\small \Delta x$ or $\small \Delta y$.

Equation (2.1.4) indicates that when an amount $\small \Delta x$ of one token is swapped for an amount $\small \Delta y$ of another token within the price range $\small (P_a, P_b)$, the average exchange price is $\small \sqrt{P_a * P_b}$.

2.2 One-Side Liquidity​

The Unibuy protocol inherits the virtual liquidity design from Uniswap v3/v4, where all liquidity is divided into different tick intervals, i.e., price ranges. Within one tick interval, the virtual liquidity constant $\small L$ remains unchanged. During trading, when the price of the token pair changes and crosses a tick boundary, the liquidity constant $\small L$ is adjusted based on the information recorded for the crossed tick.

However, there are significant differences between the Unibuy protocol and the Uniswap protocol. In Uniswap, trading within a tick interval is bidirectional, whereas in Unibuy, trading within a tick interval is unidirectional. This fundamental difference means that in Unibuy, liquidity only exists above the current price of the trading pair, while in Uniswap v3, liquidity can be distributed across the entire price range. The figure below illustrates the liquidity distribution in the Unibuy Protocol.

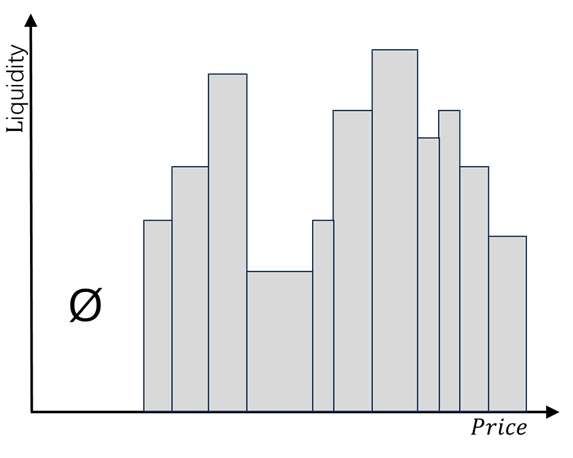
In the Uniswap protocol, the same trading pair supports mutual exchange between $\small token_0$ and $\small token_1$. Liquidity providers supply liquidity for trading, and trading users pay a transaction fee of approximately $\small 0.3\%$. The liquidity providers earn this fee, while Uniswap takes a small portion of the fee, or in some cases, none at all.

In the Unibuy protocol, there is no role of liquidity provider. All trading liquidity comes from user's maker orders. Maker orders require providing only one type of token, defined in the protocol as $\small token_0$. Taker orders always exchange $\small token_1$ for $\small token_0$ from the trading pair.

The functionality of buying or selling $\small token_0/token_1$ is actually implemented through two interconnected, mirrored, unidirectional trading pairs. The operations in Uniswap, adding liquidity, removing liquidity, and swapping, correspond to placing maker order, withdrawing maker order, and placing taker order in Unibuy. From the user’s perspective, Unibuy offers a trading experience closer to that of centralized exchanges.

In the Unibuy protocol, taker orders incur a transaction fee, while maker orders are free and charge no transaction fee, regardless of whether the order is filled or not. All transaction fees coming from taker orders go entirely to the Unibuy project.

2.3 One-way Trading Pairs​

A DEX protocol always need to provide two-way trading. The Unibuy protocol's two-way functionality is implemented through two linked, mirrored, unidirectional trading pairs. In these two linked pairs, the definitions of $\small token_0$ and $\small token_1$ are reversed. For example, given two assets, Token A/B, in one trading pair, Token A is defined as $\small token_0$, and Token B as $\small token_1$. In the mirrored pair, Token A becomes $\small token_1$, and Token B becomes $\small token_0$.

Due to this symmetry, the logic for both mirrored pairs is identical: swapping users always use $\small token_1$ to exchange for $\small token_0$ being sold by maker orders. These mirrored unidirectional pairs are merely an internal technical implementation, and users (both placing maker orders and taker orders) do not need to be aware of this technical detail, and it does not affect the user experience.

When placing a maker order, the users specify a price range and the amount of $\small token_0$ to sell. All maker orders are aggregated together to form the trading pair's liquidity. When a user places a taker order, their counterparty is the liquidity of aggregated maker orders. Since taker orders always exchange $\small token_1$ for $\small token_0$, the price of $\small token_0$ always increases unidirectionally.

The price range specified in a maker order can be above or below the current price of the trading pair. However, the lower bound of the price range, after being mirrored, must not exceed the current price of the mirrored trading pair (which is the reciprocal of the current price in the original pair). The reason for this constraint is that if it exceeds the mirrored pair’s current price, that portion of the order could be immediately filled in the mirrored pair.

The Unibuy protocol checks the user's specified price range and the current state of the trading pair to determine whether to treat the order as a taker order or as a maker order. If necessary, the protocol can partially execute the order as a taker order, and then treat the unfilled portion as a maker order.

If the lower bound of a maker order’s price range is below the current price of the trading pair, the lower price will become the current price of the trading pair after the transaction is completed, which will become the starting price for subsequent taker orders. However, if the lower bound is above the current price, the trading pair’s current price remains unchanged.

3. Unibuy Internal Mechanism​

While the design of Unibuy's one-way trading pair can effectively addresses issues such as sandwich attacks and protocol revenue, it also introduces some complexity in aggregating liquidity from different maker orders and correctly calculating the proceeds of filled maker orders. Unibuy protocol designs a few mechanisms to manage this complexity, mainly including the liquidity rebalancing mechanism and the internal exchange compensation mechanism.

3.1 Liquidity Rebalancing Mechanism​

When a user places a maker order with a specified price range $\small (P_l, P_u)$, and the lower bound $\small P_l$ is below the current price $\small P_0$ of the trading pair, the liquidity rebalancing mechanism is triggered. The reason is that in the current price range of the trading pair, some liquidity may have already been partially filled, if the price range of the new maker order overlaps with the current price range, these two sets of liquidity cannot be directly aggregated. Therefore, the partially filled liquidity must be rebalanced into the appropriate price range before aggregation can occur. Additionally, once the new maker order is published, $\small P_l$ becomes the new current price of the trading pair (if $\small P_l \leqslant P_0$), which also requires the existing liquidity in the current price range to be rebalanced for future aggregation.

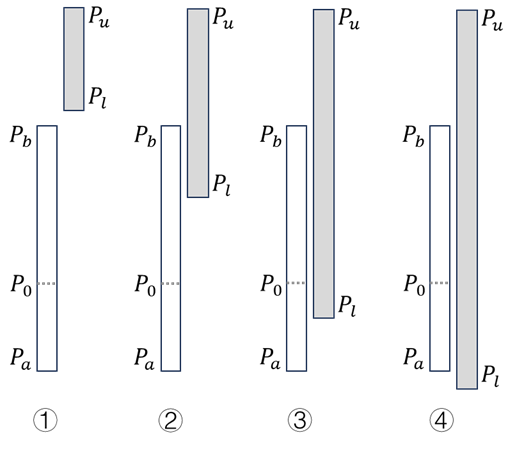
The newly added liquidity, relative to the current price range, can fall into 10 different cases as illustrated in Figure 3. Among these:

Cases 1/2/5: Since $\small P_l > P_0$ (i.e., the lower bound of the order’s price range is higher than the current price), no rebalancing is triggered.

The remaining cases require rebalancing as follows:

Cases 4/7/10: Need to rebalance to the lower bound of the current liquidity range, $\small P_a$.

Cases 8/9: Need to rebalance to the upper bound of the new liquidity range, $\small P_u$.

Cases 3/6: Need to rebalance to the lower bound of the new liquidity range, $\small P_l$.

After rebalancing, the upper bound $\small P_b$ of the price range, remains unchanged. The lower bound of the rebalanced price range, denoted as $\small P_r$, is determined by the following formula:

where $\small tick_a, tick_b, tick_0, tick_u, tick_l$ are the $\small ticks$ corresponding to the prices $\small P_a, P_b, P_0, P_u, P_l$, respectively. This formula only applies when $\small tick_l \leqslant tick_0$, no rebalancing is needed when $\small tick_l > tick_0$.

In the above formula, the evaluation order for $\small P_r$ is $\small P_u \gt P_l \gt P_a$, meaning that if the $\small P_u$ condition is met, then $\small P_r = P_u$; otherwise, if the $\small P_l$ condition is met, then $\small P_r = P_l$; otherwise, $\small P_r = P_a$.

When $\small P_r = P_u$ or $\small P_l$, the current liquidity range needs to be split first and the liquidity between $\small (P_a, P_r)$ is treated as fully filled.

Assume the current price of the trading pair is $\small P_0$, the new price range after rebalancing is $\small (P_{r}, \ P_{b})$, and the liquidity of the current liquidity range is $\small L_1$. Since the current price is $\small P_{0}$, this means that only the portion between $\small (P_0, P_b)$ still has liquidity; the portion between $\small (P_a, P_0)$ has already been sold out. The purpose of rebalancing is to redistribute the unsold $\small token_0$ across the new full price range $\small (P_{r}, P_{b})$, so that it can be aggregated with the newly added liquidity. After rebalancing, since the amount of $\small token_0$ available for sale in the new price range remains unchanged, according to formula $\small (2.1.2)$, the new virtual liquidity $\small L_2$ satisfies:

And also have:

Rebalancing is the process of redistributing the remaining untraded liquidity in the current price range to the new full price range $\small (P_r, P_b)$. The $\small LiquidityNet$ in the $\small tickInfo$ structure corresponding to the lower end $\small tick_r$ will be updated to $\small L_{2}$. The net liquidity reduction after rebalancing is $\small L_1 - L_2$.

The rebalancing mechanism not only affects the liquidity of the current price range, but also the price of the trading pair. After rebalancing, the lower bound of the newly added liquidity becomes the new current price of the trading pair. If no rebalancing occurs, the trading pair’s price remains unchanged. In the Unibuy protocol, user's takers order always cause the price of the trading pair to move upward, whereas users' maker orders may cause the price of the trading pair to fall due to the addition of liquidity with lower price.

Due to the design of the rebalancing mechanism, a user's liquidity within the price range of $\small (P_a, P_b)$ is not guaranteed to be sold ultimately at the average price of $\small \sqrt{P_a * P_b}$. After multiple rebalancings, the actual average selling price $\small P_m$ of $\small token_0$ will satisfy $\small P_a < P_m \leqslant \sqrt{P_a * P_b}$. This design allows liquidity to be traded as quickly as possible within the specified price range while still ensuring the best favorable price due to the constraint of the constant product pricing curve.

3.2 Internal exchange Compensation Mechanism​

When a user places a maker order, the newly added liquidity is aggregated with existing liquidity to serve as the counterparty of taker orders. However, the existing liquidity in that price range may have already been partially filled, and its remaining $\small token_0$ has been redistributed across the entire price range via the rebalancing mechanism. However, the newly added liquidity is completely unfilled within that price range, and therefore has a different intrinsic value from the existing liquidity. Furthermore, due to the constraints of the constant product pricing mechanism, these two types of liquidity must be aggregated together and treated uniformly for the processing of taker orders. To resolve this issue, the Unibuy protocol introduces the internal exchange compensation mechanism. While recognizing the value advantage of earlier maker orders, this mechanism ensures that liquidity from different orders with different trading states own an internally consistent value, and can be uniformly involved in taker order processing and the correct calculation of the intrinsic value of different orders when settling each maker order.

This internal exchange compensation mechanism only applies to price ranges that have been partially filled. Price ranges that are either completely unfilled or fully filled do not require compensation processing.

Assume that before adding liquidity, the total liquidity in the price range is $\small L_1$, which has been partially traded, and the amount of $\small token_1$ received is $\small R$. After rebalancing, the remaining net liquidity is $\small L_2$. Let the newly added liquidity be $\small L_d$. After the addition of the new liquidity, the total liquidity in the liquidity range is $\small L_1 + L_d$, the total net liquidity is $\small L_2 + L_d$, and the amount of $\small token_1$ received remains $\small R$. The status are summarized as the following table:

Since a user's asset entitlement is always calculated proportionally to their share of total liquidity, if a later user (hereinafter referred to as user $\small 2$) adds liquidity and then withdraws it immediately, the amount of $\small token_1$ the user would receive, denoted as $\small R_x$, is:

The withdrawn liquidity would be $\small L_d * (L_2+ L_d) / (L_1+ L_d)$. Compared with the initial liquidity $\small L_d$ added by user $\small 2$, the liquidity has decreased. The amount of liquidity reduction, denoted as $\small L_x$, is:

This reduction in liquidity corresponds to a reduction in $\small token_0$, meaning that user 2 has effectively exchanged part of their $\small token_0$ for $\small token_1$ of amount $\small R_x$. This is referred to as an internal exchange. The amount of $\small token_0$ corresponding to the reduced liquidity $\small L_x$, denote as $\small S_x$ (equivalent to the amount of $\small token_0$ effectively exchanged when user 2 immediately withdraws) is:

After successfully withdrawing the order, user $\small 2$ effectively exchanges $\small S_x$ of $\small token_0$, corresponding to the liquidity $\small L_x$ within the price range $\small (P_r, P_b)$, for $\small R_x$ of $\small token_1$. Since the liquidity value of $\small (L_1 - L_2)$ in $\small token_0$ is equivalent to amount $\small R$ of $\small token_1$, this internal exchange is value-equivalent and reasonable. It's easy to verify that $\small R_x = S_x * \sqrt{P_r * P_0}$, where $\small \sqrt{P_r * P_0}$ is the average price of this internal exchange between $\small token_0$ and $\small token_1$.

Accordingly, after the order is withdrawn, the liquidity in this price range has increased by $\small L_x$, that is $\small L_x$, relative to the liquidity $\small L_2$ before the new order was added. However, the amount of $\small token_1$ becomes $\small R * L_1 / (L_1 + L_d)$, which is reduced by $\small R_x$ compared to the original amount $\small R$. This is equivalent for the liquidity range to exchange $\small R_x$ of $\small token_1$ for the liquidity of $\small token_0$ of equal value in the same range.

Although this internal exchange is equivalent in value based on the state of the trading pair at the time of liquidity rebalancing, it is unfair to the early maker order users (collectively referred as user 1 hereinafter). The reason is that whenever the internal exchange is triggered, user 1’s filled liquidity has always been sold at a price higher than the current price of the pool or the lower price bound of user 2’s maker order. Without a reasonable compensation mechanism for user 1, it would effectively mean that user 2 exchanges a certain amount of $\small token_0$ for $\small token_1$ at a price higher than the current pair price, leading to an invisible unfair arbitrage at the expense of user 1. To address this problem, the Unibuy protocol introduces an internal exchange compensation mechanism, requiring user 2 to compensate user 1 according to defined rules. This mechanism eliminates the unfairness of hidden arbitrage and provides user 1 with a certain first-mover advantage. On centralized exchanges, orders are matched based on the order they are placed, giving earlier orders first-mover advantage. However, the Unibuy protocol doesn't prioritize user orders on the placement time, instead users' first-mover advantage is realized through an internal exchange compensation mechanism.

The compensation of the Unibuy protocol consists of two parts: one is the internal exchange fee compensation, denoted by $C_a$; the other one is the internal exchange price difference compensation, denoted by $C_b$. They are explained in the following sections.

3.2.1 Internal Exchange Fee Compensation​

The Unibuy protocol stipulates that user $\small 2$ who place maker order later in the Unibuy protocol must pay an internal exchange fee compensation based on the preset internal exchange compensation fee rate and the internal exchange amount. The internal exchange compensation is paid in $\small token_1$. Assuming the exchange compensation fee rate is $\small r$, the internal exchange fee compensation amount is:

Since the internal exchange fee compensation is proportionally distributed across all liquidity recorded in $\small tickInfo$, including user $\small 2$ also, in order to ensure that user $\small 1$ receives the above compensation, the nominal compensation paid by user $\small 2$ is:

It is easy to verify that the amount of $\small token_1$ received by user $\small 1$ in proportion is:

The first term in the above equation is the $\small token_1$ transaction proceeds that user $\small 1$ should receive without considering compensation, and the second term is the obtained internal exchange fee compensation, which is $\small C^{'}_{a}$ in $\small (3.2.1.1)$.

The amount of $\small token_1$ user $\small 2$ receives in proportion is:

The second term in the above equation is precisely the internal exchange fee compensation paid by user $\small 2$. In the Unibuy protocol implementation, the actually recorded and processed compensation amount is $\small C_{a}$, not $\small C^{'}_{a}$. The internal exchange compensation fee rate is generally set as $\small 0.2\%$.

3.2.2 Internal Exchange Price Difference Compensation​

As described above, if the price range of a new order overlaps with that of an already partially filled order, a compensation mechanism is required to prevent unreasonable arbitrage possibilities. When new and existing liquidity are aggregated, the implied internal exchange amount, denominated in $\small token_1$, is $\small R_x$ as defined in section $\small (3.2.1)$.

The Unibuy protocol stipulates that this internal exchange is valued at the current price $\small P_0$ of the trading pair. $\small P_0$ refers to the price after this maker order is added to the trading pair, specifically, which is the lower of either the lower bound of the order’s price range or the trading pair’s current price at the time of order placement.

Although the average trade price of $\small R_x$ is $\small \sqrt{P_a * P_x}$, where $\small P_x$ is the trading pair’s price $\small P_0$ at the time of liquidity rebalancing and $\small P_a$ is the $\small P_r$ mentioned in section (3.1), because $\small P_x$ is uncertain, Unibuy uses the upper bound price $\small P_b$ of the price range $(P_a, P_b)$ to calculate the nominal value of $\small R_x$.

Due to the arbitrage opportunity arising from the price difference between $\small P_0$ and $\small \sqrt{P_a * P_b}$, user $\small 2$ must compensate the earlier liquidity providers in the form of an internal exchange price difference compensation. Assuming this compensation value is represented by $\small C_b$, $\small C_b$ should satisfy the following formula:

The underlying logic of this equation is that, after applying the price difference compensation, the ratio of user $\small 2$’s actual $\small token_1$ proceeds to their nominal proceeds should align with the price ratio $\small P_0 / \sqrt{P_a * P_b}$. Simplifying the equation yields $\small C_b$ as:

3.2.3 Total Internal Exchange Compensation​

$\small C_a$ and $\small C_b$ together make up the total compensation that user $\small 2$ needs to pay, denoted as $\small C$:

When a user places a maker order, its price range may overlap and aggregate with multiple partially filled liquidity ranges. The Unibuy protocol will calculate the compensation amounts for all aggregated price ranges associated with this order and record the cumulative compensation amount in the order’s position record. When the user withdraws or liquidates the order, the protocol first calculates the total amount of $\small token_1$ the user should receive based on their share of the liquidity, then deducts the total compensation amount to determine the final $\small token_1$ amount received by the user.

A price range may receive multiple new maker orders over time, and each time the compensation amount is calculated according to the rules above. The $\small tickInfo$ field of each $\small tick$ records both the total $\small token_1$ order proceeds and the total compensation amount.

Although the internal exchange compensation is included in the proceeds calculation when a user withdraws liquidity, it is zero-sum in nature. The total sum of compensation proceeds across all liquidity price ranges must exactly equal to the total amount of internal exchange compensations recorded as deductions in all users’ order information. These amounts offset each other. The internal exchange compensation is merely an internal mechanism of the protocol, and does not affect unrelated liquidity price ranges. It is completely transparent to taker orders, only requiring processing when a user places or withdraws a maker order.

3.3 Liquidity Range Splitting​

When a user places an order, if the given price range $\small (P_l, P_u)$ has its lower and/or upper boundary $\small P_l$ or $\small P_u$ located inside an existing liquidity range $\small (P_a, P_b)$, and that liquidity range is partially filled, the liquidity range must be split. Specifically, the original range is divided into two sub-ranges: $\small (P_a, P_s)$ and $\small (P_s, P_b)$, where $\small P_s$ is $\small P_u$ and/or $\small P_l$. The purpose of liquidity range splitting is to enable liquidity aggregation. When splitting, the amount $\small R$ of $\small token_1$ received from the partial fill is divided into upper and lower portions $\small R_u$ and $\small R_l$ according to the following formulas:

If there are internal exchange compensation fees in this liquidity range, they must also be split according to the same rules.

3.4 Technical Implementation​

The following describes the key technical aspects of the Unibuy protocol at the smart contract implementation level.

3.4.1 Global State​

Within the Unibuy smart contract, each trading pair maintains the following global state variables:

Each trading pair maintains a global height parameter $\small H_g$, starting from 1. Whenever the trading pair’s price rises and crosses an upper $\small tick$, $\small H_g$ increases by 1. When a user places a maker order, the value of $\small H_g$ at that time is recorded in the order information. When the user settles the order, the protocol refers to this recorded value and the current $\small H_g$ to determine the order’s execution status.

$\small P_0$ is the current price of the trading pair, and $\small I_t$ is the $\small tick$ value corresponding to this price.

$\small F_t$ is the taker order fee rate, with a default value of 30 basis points (0.3%), charged in $\small token_0$.

$\small F_m$ is the maker order overdue fee rate. Placing and withdrawing maker orders is free, but if a maker order has been fully filled and the proceeds are not withdrawn for a long time, an overdue withdrawal fee is charged. This fee is charged proportionally to the $\small token_1$ amount received from the order execution.

$\small F_o$ is the internal exchange compensation fee rate for maker orders, also charged in $\small token_1$.

$\small G_t$ is the maximum gap allowed for a maker order’s price range $\small (P_l, P_u)$. Because placing a maker order can trigger the internal exchange compensation mechanism, the larger the price gap, the more such processing may occur, and the higher the on-chain costs. Therefore, a maximum price gap is set as a restriction. If users truly want to place a maker order with a larger price gap, they can split it into multiple orders.

3.4.2 Tick Status​

The contract stores a mapping from $tick$ index to $\small tickInfo$ structure. The format of $\small tickInfo$ is as follows:

A $\small tickInfo$ may have two different states: one is that the liquidity is not traded at all, and the other is that the liquidity is partially traded.

When the liquidity has never been traded, $\small L_g$ represents the total liquidity of all orders that use this $\small tick$ as a price boundary. $\small L_n$ represents the net liquidity of all orders that use this $\small tick$ as a price boundary, i.e., the change of liquidity when crossing this $\small tick$. In this case, $\small R_r, R_o$ are meaningless and are set to 0.

When liquidity has been partially traded, $\small L_g$ represents the total liquidity of the price range above this $\small tick$. $\small L_n$ represents the remaining net liquidity of this price range after liquidity rebalancing. $\small R_r$ represents the amount of $\small token_1$ received after partial trades in this liquidity range. $\small R_o$ represents the sum of all internal exchange compensation and forward price difference compensation from orders placed later.

$\small P_t$ is the price corresponding to this $\small tick$. Pre-storing this price helps optimize trading performance.

$\small H_t$ is the minimum $\small poolHeight$ among all liquidity orders associated with this $\small tick$. When crossing this liquidity range, $\small H_t$ is stored as $\small X_t$ (see section $\small 3.4.3$) in the corresponding liquidation list item.

When the price crosses upward through a price range, $\small L_g, L_n, R_r, R_o, H_t$ in the lower $\small tick$ will be cleared, and $\small L_g$, $\small L_n$, $\small R_r$, $\small R_o$, $\small H_t$ in the upper $\small tick$ will be updated.

$\small C_t$ is the record of all $\small H_g$ values where this $\small tick$ has been crossed upward. When the price crosses this $\small tick$ upward, the global $\small H_g$ is appended to $\small C_t$. When all liquidity corresponding to a certain height in the liquidation list has been withdrawn, that height is removed from $\small C_t$. If $\small C_t$ has a total length of 0 and $\small L_g$ is also 0, this $\small tick$ is marked as uninitialized.

3.4.3 Liquidation List​

The contract maintains a mapping from $\small H_g$ to the trading result of the crossed $\small tick$, which is used to calculate the user's proceeds when they withdraw the order.

$\small L_s$ is the total sold liquidity in the current price range when the price crosses upward through the $\small tick$.

$\small R_r$ is the total amount of $\small token_1$ received from selling the total liquidity.

Maker order users share $\small R_r$ proportionally based on the liquidity of their orders. The value of $\small R_r$ is the sum of the amount of $\small token_1$ received from directly selling $\small token_0$, and all compensation received.

$\small X_t$ is the value of $\small H_t$ of the corresponding $\small tickInfo$ when the price crosses this $\small tick$.

3.4.3 Maker Order Information​

The user's maker order includes the following information:

$\small L_p$ is the liquidity of the order. $\small H_p$ is the current height of the trading pair at the time the order was placed. $\small D_p$ is the total compensation for the order, including the internal exchange fee compensation and the price difference compensation. This amount is a virtual amount that is deducted from the $\small token_1$ amount received by the user when the maker order is withdrawn.

The price range of the maker order and the index of the trading pair are encoded in the mapping index of the maker order information. They do not need to be explicitly stored in the trading pair itself, instead the Unibuy router contract will store them.

4. Orders​

When placing an order, the user must specify the two assets to be traded, $\small token_0$ and $\small token_1$, as well as the buy or sell price and amount. The Unibuy contract will automatically match the specified tokens and trading intent with the corresponding unidirectional trading pair and determine whether the price range can be processed as a taker order. If the price is suitable, the order will be filled immediately as a taker order, if not, the order will be processed as a maker order. If the order can only be partially filled, the filled portion will be executed as a taker order first, and the unfilled portion can either be canceled or placed as a maker order.

4.1 Maker Order​

A maker order is the order that cannot be filled immediately, and needs to be aggregated with the existing liquidity of the trading pair, waiting for following taker orders to be filled. Maker orders may trigger the internal exchange and the correlated compensation processing within a price range, which may require the user to pay a certain amount of compensation in $\small token_1$. This compensation does not need to be paid upfront, instead, it is deducted from the order’s execution proceeds when the order is eventually filled. Even if a maker order is never filled, the internal exchange proceeds is sufficient to cover the compensation. This compensation is not a loss for the user, but rather a reasonable value balance to prevent internal arbitrage possibility.

The price range specified for a maker order must not be higher than the price of the mirror trading pair. Any portion above this threshold can be immediately filled in the mirror pair, and the contract will perform the corresponding checks.

4.2 Order Withdraw​

A user may withdraw their own maker order at any time, regardless whether it is unfilled, partially filled, or fully filled.

Even if a maker order has never been filled, the amount of $\small token_0$ the user receives upon withdrawing may not be exactly the same as the amount originally deposited. If the order has triggered the internal exchange and the forward compensation mechanism, the user may receive a reduced amount of $\small token_0$ along with a certain amount of $\small token_1$.

If a maker order has been fully filled, the user is required to withdraw it in time, typically within one week. If withdrawn within a week, there is no fee. After one week, the protocol allows third parties to withdraw the order on behalf of the user, in which case the user must pay a withdrawing service fee, typically $\small 0.2\%$ of the amount of $\small token_1$ received. The Unibuy protocol team will also provide this service. This feature prevents a lot of fully filled orders from accumulating in the contract, which would otherwise degrade the performance of maker order placing and withdrawing.

4.3 Taker Order​

When an order can be partially or fully filled immediately, it is processed as a taker order. Taker order is required to pay a transaction fee, typically $\small 0.3\%$, paid in $\small token_1$. Taker orders are filled immediately. If the order cannot be fully filled immediately, the user may specify one of the following handling methods:

1. Partially filled, cancel the rest.
2. Partially filled, place the rest as a maker order.
3. Do not fill at all, cancel the entire order.

4.4 Order Chaining​

Order chaining allows a user, when placing a maker order, to specify that if the order is fully filled, the received $\small token_1$ could be treated as $\small token_0$ in the mirror trading pair and placed as a new maker order within a specified price range.

Order chaining is not executed automatically. It must be triggered by the user, a third-party service provider, or the Unibuy project team. If triggered by someone other than the user, a fee will be charged.

5. Summary​

The Unibuy protocol is a significant evolution of the constant-product AMM type of DEX protocol. It can address issues present in existing DEXs such as sandwich attacks and impermanent loss. Traditional market makers can still participate in market making within Unibuy protocol through placing maker orders or taker orders, but their trading behavior is treated the same as that of ordinary traders at the protocol level, and the protocol no longer shares trading fees with market makers. This allows the Unibuy project to earn the rightful revenue from trading fees, supporting the project’s sustainable growth. Ordinary users can place idle assets for sale as chaining maker orders to automatically to achieve buy-low-sell-high arbitrage from the market fluctuations in the way shifting the liquidiy to the mirror pair after the order is fully filled. If a large number of individual users engage in such an arbitrage, it can help mitigate market volatility and generate passive income for ordinary users.

The Unibuy protocol can offer an order book experience similar to that of centralized exchanges but without the need to custody user assets, thereby eliminating centralized custody risk. Due to the latency and discontinuity inherent in blockchain transactions, placing a maker order should be a careful and deliberate decision, reflecting the user’s true intent. Maker orders are transparently visible on-chain, helping to avoid certain misleading issues in CEXs, such as frequent placing and canceling of orders, self-trading, price manipulation.

DEX protocols will continue to evolve. The Unibuy protocol represents an exploratory breakthrough and advancement in DEX evolution, and it is believed that more and better DEX protocol innovations will continue to emerge in the future.

References​

[1] Hayden Adams, Uniswap Whitepaper, https://hackmd.io/C-DvwDSfSxuh-Gd4WKE_ig.

[2] Hayden Adams et al, Uniswap V2 Core, https://uniswap.org/whitepaper.pdf.

[3] Hayden Adams et al, Uniswap v3 Core. https://uniswap.org/whitepaper-v3.pdf.

[4] Hayden Adams et al, Uniswap v4 Core. https://uniswap.org/whitepaper-v4.pdf

[5] Balancer, Impermanent Loss

[6] flashbots, https://docs.flashbots.net/

[7] Maximal extractable value (MEV). https://ethereum.org/en/developers/docs/mev/

[8] EtherDelta, A decentralized peer-to-peer cryptocurrency exchange built on Ethereum, https://etherdelta.com

[9] Project Serum, https://projectserum.medium.com

[10] Derik Lu, Feswap Exchange, https://www.feswap.io/download